Modeltime Integration

In this tutorial you will learn how to use the Bayesmodels package and how to integrate it with the usual Modeltime workflow. The main purposes are:

• Use an Arima Bayesian model to see how it would apply in the Bayesmodels package.

• Compare the above model with the classic implementation of the Modeltime package through the usual workflow of the escosystem.

Bayesmodels unlocks the following models in one package. Precisely its greatest advantage is to be able to integrate these models with the Modeltime and Tidymodels ecosystems.

• Arima: bayesmodels connects to the bayesforecast package.

• Garch: bayesmodels connects to the bayesforecast package.

• Random Walk (Naive): bayesmodels connects to the bayesforecast package.

• State Space Model: bayesmodels connects to the bayesforecast and bsts packages.

• Stochastic Volatility Model: bayesmodels connects to the bayesforecast package.

• Generalized Additive Models (GAMS): bayesmodels connects to the brms package.

• Adaptive Splines Surface: bayesmodels connects to the BASS package.

• Exponential Smoothing: bayesmodels connects to the Rglt package.

The Modeltime Workflow

Here’s the general process and where the functions fit.

The Modeltime Workflow

Just follow the modeltime workflow, which is detailed in 6 convenient steps:

1. Collect data and split into training and test sets
2. Create & Fit Multiple Models
3. Add fitted models to a Model Table
4. Calibrate the models to a testing set.
5. Perform Testing Set Forecast & Accuracy Evaluation
6. Refit the models to Full Dataset & Forecast Forward

Let’s go through a guided tour to kick the tires on modeltime.

Time Series Forecasting Example

Load libraries to complete this short tutorial.

library(tidymodels)
library(bayesmodels)
library(modeltime)
library(tidyverse)
library(timetk)
library(lubridate)
# This toggles plots from plotly (interactive) to ggplot (static)
interactive <- FALSE

Step 1 - Collect data and split into training and test sets.

# Data
m750 <- m4_monthly %>% filter(id == "M750")

We can visualize the dataset.

m750 %>%
  plot_time_series(date, value, .interactive = interactive)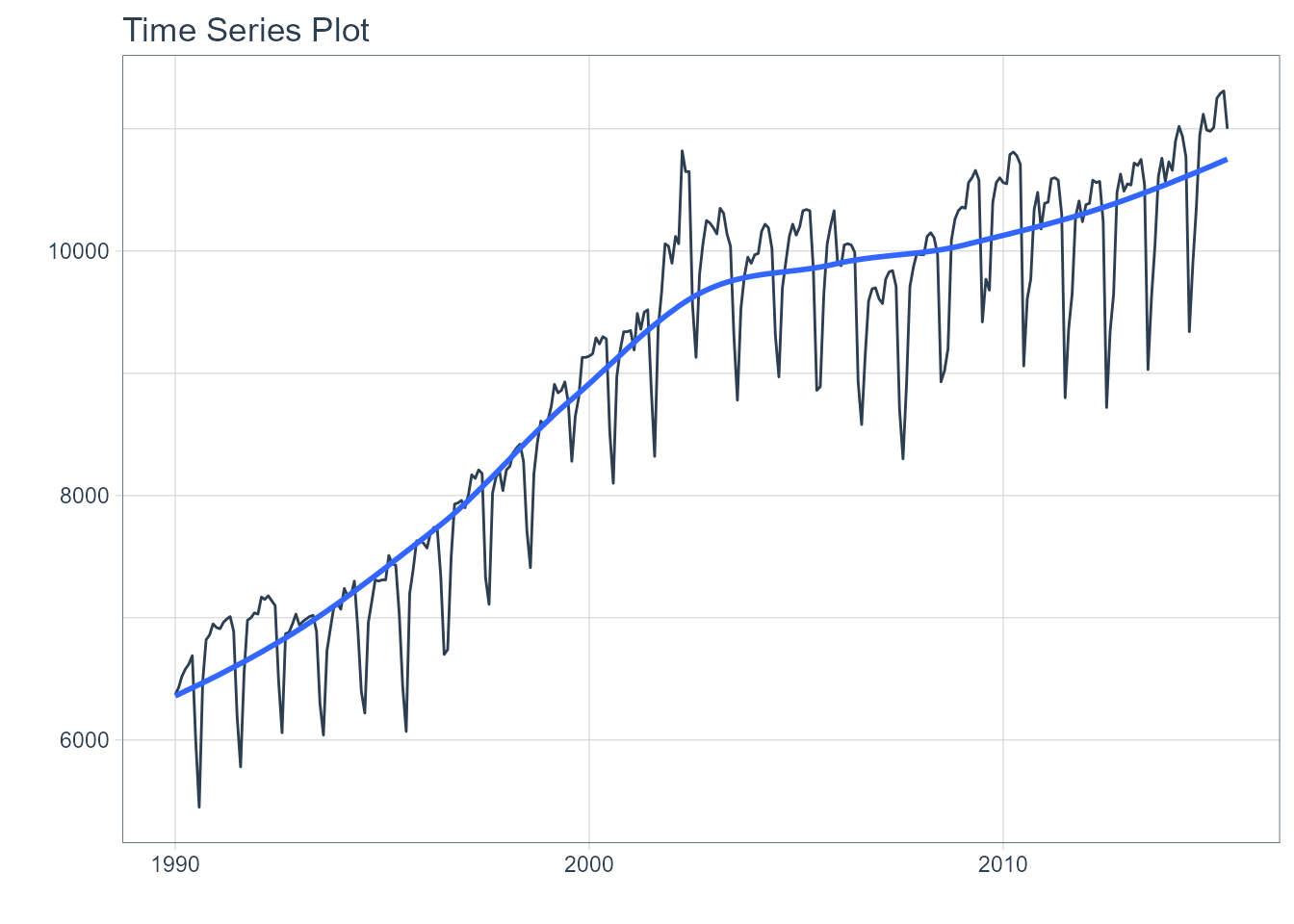

Let’s split the data into training and test sets using initial_time_split()

# Split Data 80/20
splits <- initial_time_split(m750, prop = 0.9)

Step 2 - Create & Fit Multiple Models

We can easily create dozens of forecasting models by combining bayesmodels, modeltime and parsnip. We can also use the workflows interface for adding preprocessing! Your forecasting possibilities are endless. Let’s model a couple of arima models:

Important note: Handling Date Features

Bayesmodels and Modeltime models (e.g. sarima_reg() and arima_reg()) are created with a date or date time feature in the model. You will see that most models include a formula like fit(value ~ date, data).

Parsnip models (e.g. linear_reg()) typically should not have date features, but may contain derivatives of dates (e.g. month, year, etc). You will often see formulas like fit(value ~ as.numeric(date) + month(date), data).

Model 1: ARIMA (Modeltime)

First, we create a basic univariate ARIMA model using “Arima” using arima_reg()

# Model 1: arima ----
model_fit_arima<- arima_reg(non_seasonal_ar = 0,
                            non_seasonal_differences = 1,
                            non_seasonal_ma = 1,
                            seasonal_period = 12,
                            seasonal_ar = 0,
                            seasonal_differences = 1,
                            seasonal_ma = 1) %>%
    set_engine(engine = "arima") %>%
    fit(value ~ date, data = training(splits))

Model 2: ARIMA (Bayesmodels)

Now, we create the same model but from a Bayesian perspective with the package bayesmodels:

# Model 2: arima_boost ----
model_fit_arima_bayes<- sarima_reg(non_seasonal_ar = 0,
                                  non_seasonal_differences = 1,
                                  non_seasonal_ma = 1,
                                  seasonal_period = 12,
                                  seasonal_ar = 0,
                                  seasonal_differences = 1,
                                  seasonal_ma = 1,
                                  pred_seed = 100) %>%
    set_engine(engine = "stan") %>%
    fit(value ~ date, data = training(splits))
#> 
#> SAMPLING FOR MODEL 'Sarima' NOW (CHAIN 1).
#> Chain 1: 
#> Chain 1: Gradient evaluation took 0 seconds
#> Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0 seconds.
#> Chain 1: Adjust your expectations accordingly!
#> Chain 1: 
#> Chain 1: 
#> Chain 1: Iteration:    1 / 2000 [  0%]  (Warmup)
#> Chain 1: Iteration:  200 / 2000 [ 10%]  (Warmup)
#> Chain 1: Iteration:  400 / 2000 [ 20%]  (Warmup)
#> Chain 1: Iteration:  600 / 2000 [ 30%]  (Warmup)
#> Chain 1: Iteration:  800 / 2000 [ 40%]  (Warmup)
#> Chain 1: Iteration: 1000 / 2000 [ 50%]  (Warmup)
#> Chain 1: Iteration: 1001 / 2000 [ 50%]  (Sampling)
#> Chain 1: Iteration: 1200 / 2000 [ 60%]  (Sampling)
#> Chain 1: Iteration: 1400 / 2000 [ 70%]  (Sampling)
#> Chain 1: Iteration: 1600 / 2000 [ 80%]  (Sampling)
#> Chain 1: Iteration: 1800 / 2000 [ 90%]  (Sampling)
#> Chain 1: Iteration: 2000 / 2000 [100%]  (Sampling)
#> Chain 1: 
#> Chain 1:  Elapsed Time: 1.041 seconds (Warm-up)
#> Chain 1:                0.803 seconds (Sampling)
#> Chain 1:                1.844 seconds (Total)
#> Chain 1: 
#> 
#> SAMPLING FOR MODEL 'Sarima' NOW (CHAIN 2).
#> Chain 2: 
#> Chain 2: Gradient evaluation took 0 seconds
#> Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0 seconds.
#> Chain 2: Adjust your expectations accordingly!
#> Chain 2: 
#> Chain 2: 
#> Chain 2: Iteration:    1 / 2000 [  0%]  (Warmup)
#> Chain 2: Iteration:  200 / 2000 [ 10%]  (Warmup)
#> Chain 2: Iteration:  400 / 2000 [ 20%]  (Warmup)
#> Chain 2: Iteration:  600 / 2000 [ 30%]  (Warmup)
#> Chain 2: Iteration:  800 / 2000 [ 40%]  (Warmup)
#> Chain 2: Iteration: 1000 / 2000 [ 50%]  (Warmup)
#> Chain 2: Iteration: 1001 / 2000 [ 50%]  (Sampling)
#> Chain 2: Iteration: 1200 / 2000 [ 60%]  (Sampling)
#> Chain 2: Iteration: 1400 / 2000 [ 70%]  (Sampling)
#> Chain 2: Iteration: 1600 / 2000 [ 80%]  (Sampling)
#> Chain 2: Iteration: 1800 / 2000 [ 90%]  (Sampling)
#> Chain 2: Iteration: 2000 / 2000 [100%]  (Sampling)
#> Chain 2: 
#> Chain 2:  Elapsed Time: 1.041 seconds (Warm-up)
#> Chain 2:                0.852 seconds (Sampling)
#> Chain 2:                1.893 seconds (Total)
#> Chain 2: 
#> 
#> SAMPLING FOR MODEL 'Sarima' NOW (CHAIN 3).
#> Chain 3: 
#> Chain 3: Gradient evaluation took 0 seconds
#> Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0 seconds.
#> Chain 3: Adjust your expectations accordingly!
#> Chain 3: 
#> Chain 3: 
#> Chain 3: Iteration:    1 / 2000 [  0%]  (Warmup)
#> Chain 3: Iteration:  200 / 2000 [ 10%]  (Warmup)
#> Chain 3: Iteration:  400 / 2000 [ 20%]  (Warmup)
#> Chain 3: Iteration:  600 / 2000 [ 30%]  (Warmup)
#> Chain 3: Iteration:  800 / 2000 [ 40%]  (Warmup)
#> Chain 3: Iteration: 1000 / 2000 [ 50%]  (Warmup)
#> Chain 3: Iteration: 1001 / 2000 [ 50%]  (Sampling)
#> Chain 3: Iteration: 1200 / 2000 [ 60%]  (Sampling)
#> Chain 3: Iteration: 1400 / 2000 [ 70%]  (Sampling)
#> Chain 3: Iteration: 1600 / 2000 [ 80%]  (Sampling)
#> Chain 3: Iteration: 1800 / 2000 [ 90%]  (Sampling)
#> Chain 3: Iteration: 2000 / 2000 [100%]  (Sampling)
#> Chain 3: 
#> Chain 3:  Elapsed Time: 1.003 seconds (Warm-up)
#> Chain 3:                0.788 seconds (Sampling)
#> Chain 3:                1.791 seconds (Total)
#> Chain 3: 
#> 
#> SAMPLING FOR MODEL 'Sarima' NOW (CHAIN 4).
#> Chain 4: 
#> Chain 4: Gradient evaluation took 0 seconds
#> Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0 seconds.
#> Chain 4: Adjust your expectations accordingly!
#> Chain 4: 
#> Chain 4: 
#> Chain 4: Iteration:    1 / 2000 [  0%]  (Warmup)
#> Chain 4: Iteration:  200 / 2000 [ 10%]  (Warmup)
#> Chain 4: Iteration:  400 / 2000 [ 20%]  (Warmup)
#> Chain 4: Iteration:  600 / 2000 [ 30%]  (Warmup)
#> Chain 4: Iteration:  800 / 2000 [ 40%]  (Warmup)
#> Chain 4: Iteration: 1000 / 2000 [ 50%]  (Warmup)
#> Chain 4: Iteration: 1001 / 2000 [ 50%]  (Sampling)
#> Chain 4: Iteration: 1200 / 2000 [ 60%]  (Sampling)
#> Chain 4: Iteration: 1400 / 2000 [ 70%]  (Sampling)
#> Chain 4: Iteration: 1600 / 2000 [ 80%]  (Sampling)
#> Chain 4: Iteration: 1800 / 2000 [ 90%]  (Sampling)
#> Chain 4: Iteration: 2000 / 2000 [100%]  (Sampling)
#> Chain 4: 
#> Chain 4:  Elapsed Time: 1.089 seconds (Warm-up)
#> Chain 4:                0.866 seconds (Sampling)
#> Chain 4:                1.955 seconds (Total)
#> Chain 4:

plot(model_fit_arima_bayes$fit$models$model_1)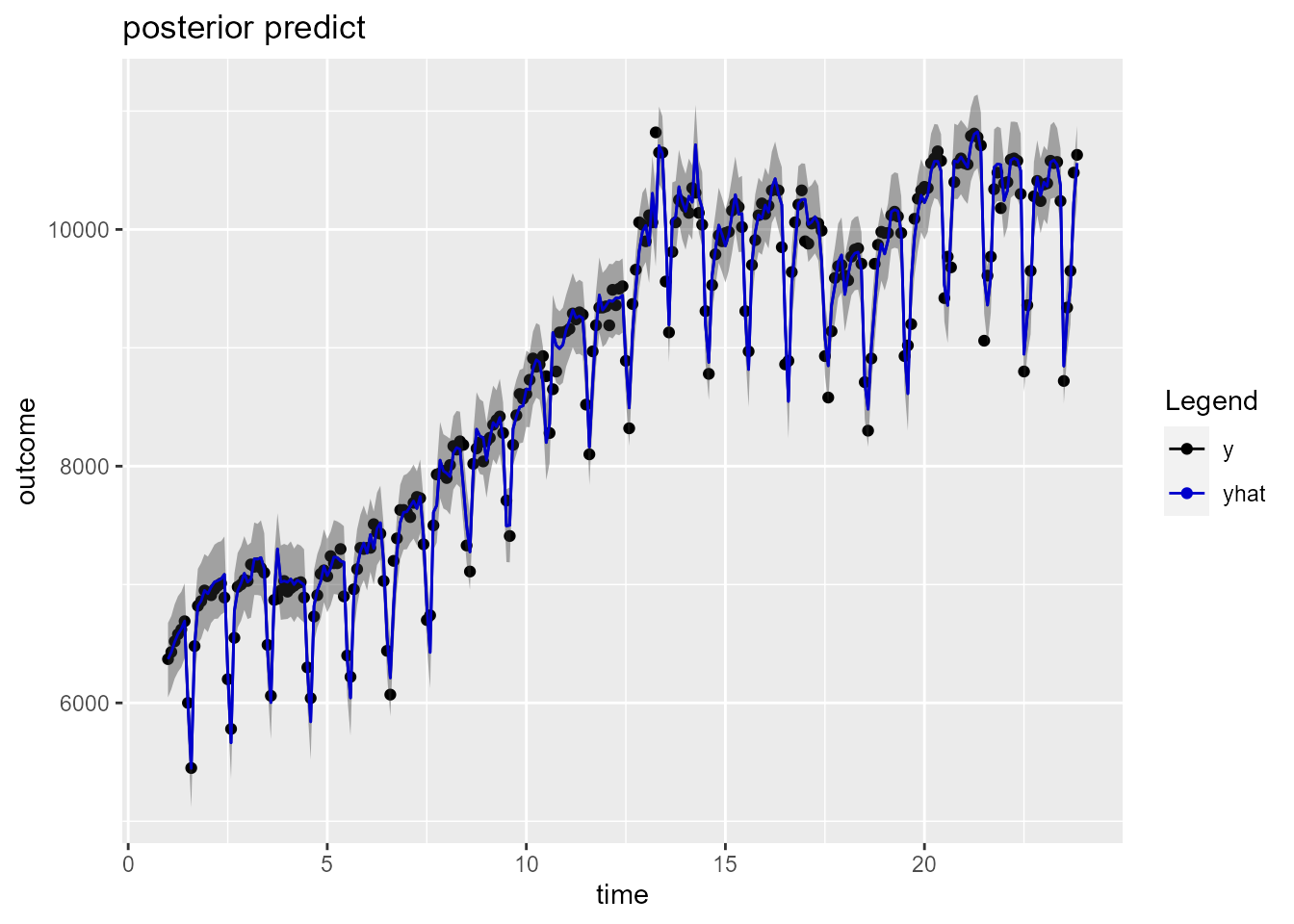

Model 3: Random Walk (Naive) (Bayesmodels)

model_fit_naive <- random_walk_reg(seasonal_random_walk = TRUE, seasonal_period = 12) %>%
                   set_engine("stan") %>%
                   fit(value ~ date + month(date), data = training(splits))
#> 
#> SAMPLING FOR MODEL 'Sarima' NOW (CHAIN 1).
#> Chain 1: 
#> Chain 1: Gradient evaluation took 0 seconds
#> Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0 seconds.
#> Chain 1: Adjust your expectations accordingly!
#> Chain 1: 
#> Chain 1: 
#> Chain 1: Iteration:    1 / 2000 [  0%]  (Warmup)
#> Chain 1: Iteration:  200 / 2000 [ 10%]  (Warmup)
#> Chain 1: Iteration:  400 / 2000 [ 20%]  (Warmup)
#> Chain 1: Iteration:  600 / 2000 [ 30%]  (Warmup)
#> Chain 1: Iteration:  800 / 2000 [ 40%]  (Warmup)
#> Chain 1: Iteration: 1000 / 2000 [ 50%]  (Warmup)
#> Chain 1: Iteration: 1001 / 2000 [ 50%]  (Sampling)
#> Chain 1: Iteration: 1200 / 2000 [ 60%]  (Sampling)
#> Chain 1: Iteration: 1400 / 2000 [ 70%]  (Sampling)
#> Chain 1: Iteration: 1600 / 2000 [ 80%]  (Sampling)
#> Chain 1: Iteration: 1800 / 2000 [ 90%]  (Sampling)
#> Chain 1: Iteration: 2000 / 2000 [100%]  (Sampling)
#> Chain 1: 
#> Chain 1:  Elapsed Time: 0.675 seconds (Warm-up)
#> Chain 1:                0.262 seconds (Sampling)
#> Chain 1:                0.937 seconds (Total)
#> Chain 1: 
#> 
#> SAMPLING FOR MODEL 'Sarima' NOW (CHAIN 2).
#> Chain 2: 
#> Chain 2: Gradient evaluation took 0 seconds
#> Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0 seconds.
#> Chain 2: Adjust your expectations accordingly!
#> Chain 2: 
#> Chain 2: 
#> Chain 2: Iteration:    1 / 2000 [  0%]  (Warmup)
#> Chain 2: Iteration:  200 / 2000 [ 10%]  (Warmup)
#> Chain 2: Iteration:  400 / 2000 [ 20%]  (Warmup)
#> Chain 2: Iteration:  600 / 2000 [ 30%]  (Warmup)
#> Chain 2: Iteration:  800 / 2000 [ 40%]  (Warmup)
#> Chain 2: Iteration: 1000 / 2000 [ 50%]  (Warmup)
#> Chain 2: Iteration: 1001 / 2000 [ 50%]  (Sampling)
#> Chain 2: Iteration: 1200 / 2000 [ 60%]  (Sampling)
#> Chain 2: Iteration: 1400 / 2000 [ 70%]  (Sampling)
#> Chain 2: Iteration: 1600 / 2000 [ 80%]  (Sampling)
#> Chain 2: Iteration: 1800 / 2000 [ 90%]  (Sampling)
#> Chain 2: Iteration: 2000 / 2000 [100%]  (Sampling)
#> Chain 2: 
#> Chain 2:  Elapsed Time: 1.36 seconds (Warm-up)
#> Chain 2:                0.292 seconds (Sampling)
#> Chain 2:                1.652 seconds (Total)
#> Chain 2: 
#> 
#> SAMPLING FOR MODEL 'Sarima' NOW (CHAIN 3).
#> Chain 3: 
#> Chain 3: Gradient evaluation took 0 seconds
#> Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0 seconds.
#> Chain 3: Adjust your expectations accordingly!
#> Chain 3: 
#> Chain 3: 
#> Chain 3: Iteration:    1 / 2000 [  0%]  (Warmup)
#> Chain 3: Iteration:  200 / 2000 [ 10%]  (Warmup)
#> Chain 3: Iteration:  400 / 2000 [ 20%]  (Warmup)
#> Chain 3: Iteration:  600 / 2000 [ 30%]  (Warmup)
#> Chain 3: Iteration:  800 / 2000 [ 40%]  (Warmup)
#> Chain 3: Iteration: 1000 / 2000 [ 50%]  (Warmup)
#> Chain 3: Iteration: 1001 / 2000 [ 50%]  (Sampling)
#> Chain 3: Iteration: 1200 / 2000 [ 60%]  (Sampling)
#> Chain 3: Iteration: 1400 / 2000 [ 70%]  (Sampling)
#> Chain 3: Iteration: 1600 / 2000 [ 80%]  (Sampling)
#> Chain 3: Iteration: 1800 / 2000 [ 90%]  (Sampling)
#> Chain 3: Iteration: 2000 / 2000 [100%]  (Sampling)
#> Chain 3: 
#> Chain 3:  Elapsed Time: 0.875 seconds (Warm-up)
#> Chain 3:                0.282 seconds (Sampling)
#> Chain 3:                1.157 seconds (Total)
#> Chain 3: 
#> 
#> SAMPLING FOR MODEL 'Sarima' NOW (CHAIN 4).
#> Chain 4: 
#> Chain 4: Gradient evaluation took 0 seconds
#> Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0 seconds.
#> Chain 4: Adjust your expectations accordingly!
#> Chain 4: 
#> Chain 4: 
#> Chain 4: Iteration:    1 / 2000 [  0%]  (Warmup)
#> Chain 4: Iteration:  200 / 2000 [ 10%]  (Warmup)
#> Chain 4: Iteration:  400 / 2000 [ 20%]  (Warmup)
#> Chain 4: Iteration:  600 / 2000 [ 30%]  (Warmup)
#> Chain 4: Iteration:  800 / 2000 [ 40%]  (Warmup)
#> Chain 4: Iteration: 1000 / 2000 [ 50%]  (Warmup)
#> Chain 4: Iteration: 1001 / 2000 [ 50%]  (Sampling)
#> Chain 4: Iteration: 1200 / 2000 [ 60%]  (Sampling)
#> Chain 4: Iteration: 1400 / 2000 [ 70%]  (Sampling)
#> Chain 4: Iteration: 1600 / 2000 [ 80%]  (Sampling)
#> Chain 4: Iteration: 1800 / 2000 [ 90%]  (Sampling)
#> Chain 4: Iteration: 2000 / 2000 [100%]  (Sampling)
#> Chain 4: 
#> Chain 4:  Elapsed Time: 0.515 seconds (Warm-up)
#> Chain 4:                0.282 seconds (Sampling)
#> Chain 4:                0.797 seconds (Total)
#> Chain 4:

plot(model_fit_naive$fit$models$model_1)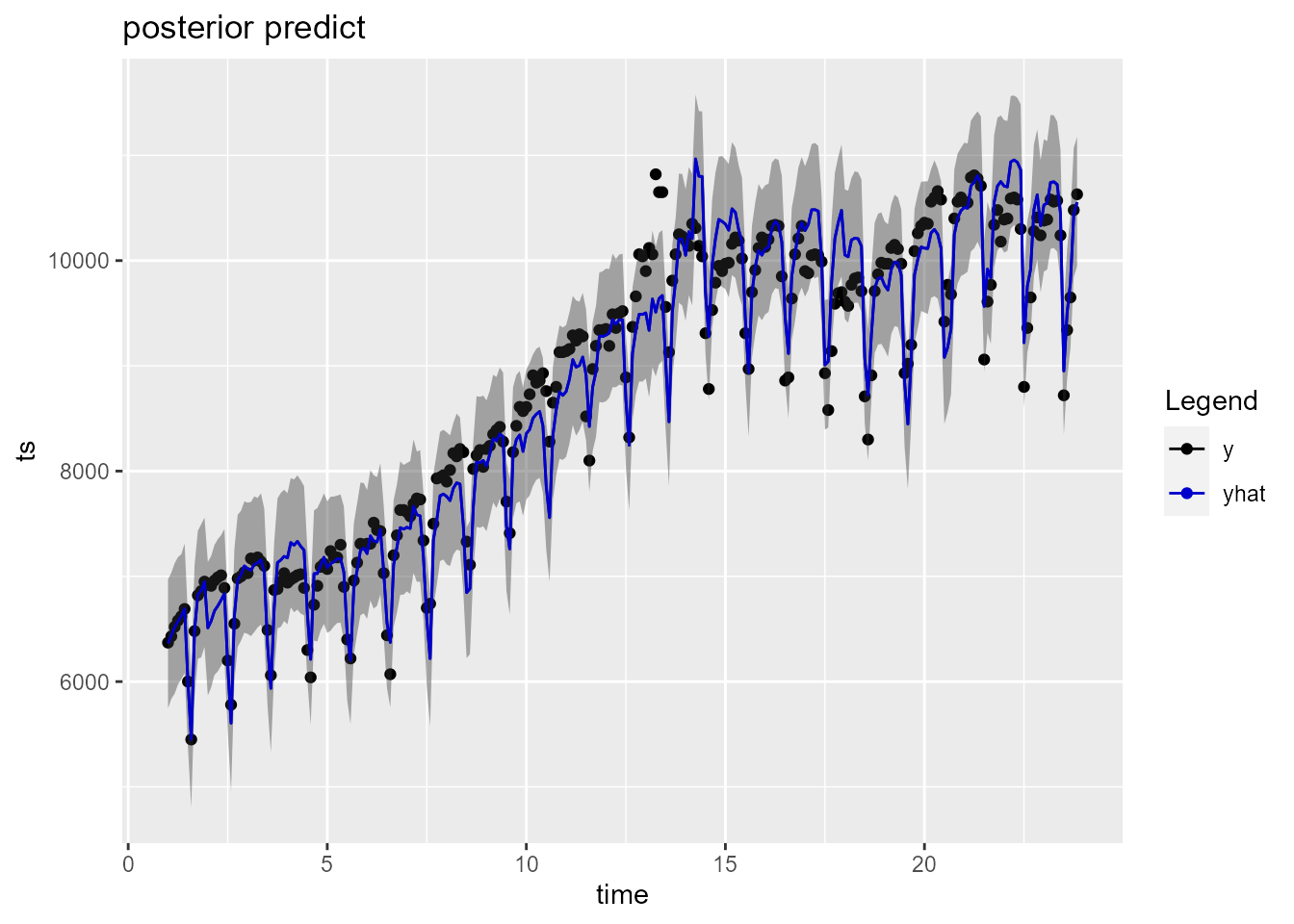

Step 3 - Add fitted models to a Model Table.

The next step is to add each of the models to a Modeltime Table using modeltime_table(). This step does some basic checking to make sure each of the models are fitted and that organizes into a scalable structure called a “Modeltime Table” that is used as part of our forecasting workflow.

We have 2 models to add.

models_tbl <- modeltime_table(
    model_fit_arima,
    model_fit_arima_bayes,
    model_fit_naive
)
models_tbl
#> # Modeltime Table
#> # A tibble: 3 x 3
#>   .model_id .model   .model_desc            
#>       <int> <list>   <chr>                  
#> 1         1 <fit[+]> ARIMA(0,1,1)(0,1,1)[12]
#> 2         2 <fit[+]> BAYESIAN ARIMA MODEL   
#> 3         3 <fit[+]> NAIVE MODEL

Step 4 - Calibrate the model to a testing set.

Calibrating adds a new column, .calibration_data, with the test predictions and residuals inside. A few notes on Calibration:

• Calibration is how confidence intervals and accuracy metrics are determined
• Calibration Data is simply forecasting predictions and residuals that are calculated from out-of-sample data.
• After calibrating, the calibration data follows the data through the forecasting workflow.

calibration_tbl <- models_tbl %>%
    modeltime_calibrate(new_data = testing(splits))
calibration_tbl
#> # Modeltime Table
#> # A tibble: 3 x 5
#>   .model_id .model   .model_desc             .type .calibration_data    
#>       <int> <list>   <chr>                   <chr> <list>               
#> 1         1 <fit[+]> ARIMA(0,1,1)(0,1,1)[12] Test  <tibble[,4] [31 x 4]>
#> 2         2 <fit[+]> BAYESIAN ARIMA MODEL    Test  <tibble[,4] [31 x 4]>
#> 3         3 <fit[+]> NAIVE MODEL             Test  <tibble[,4] [31 x 4]>

Step 5 - Testing Set Forecast & Accuracy Evaluation

There are 2 critical parts to an evaluation.

• Visualizing the Forecast vs Test Data Set
• Evaluating the Test (Out of Sample) Accuracy

5A - Visualizing the Forecast Test

Visualizing the Test Error is easy to do using the interactive plotly visualization (just toggle the visibility of the models using the Legend).

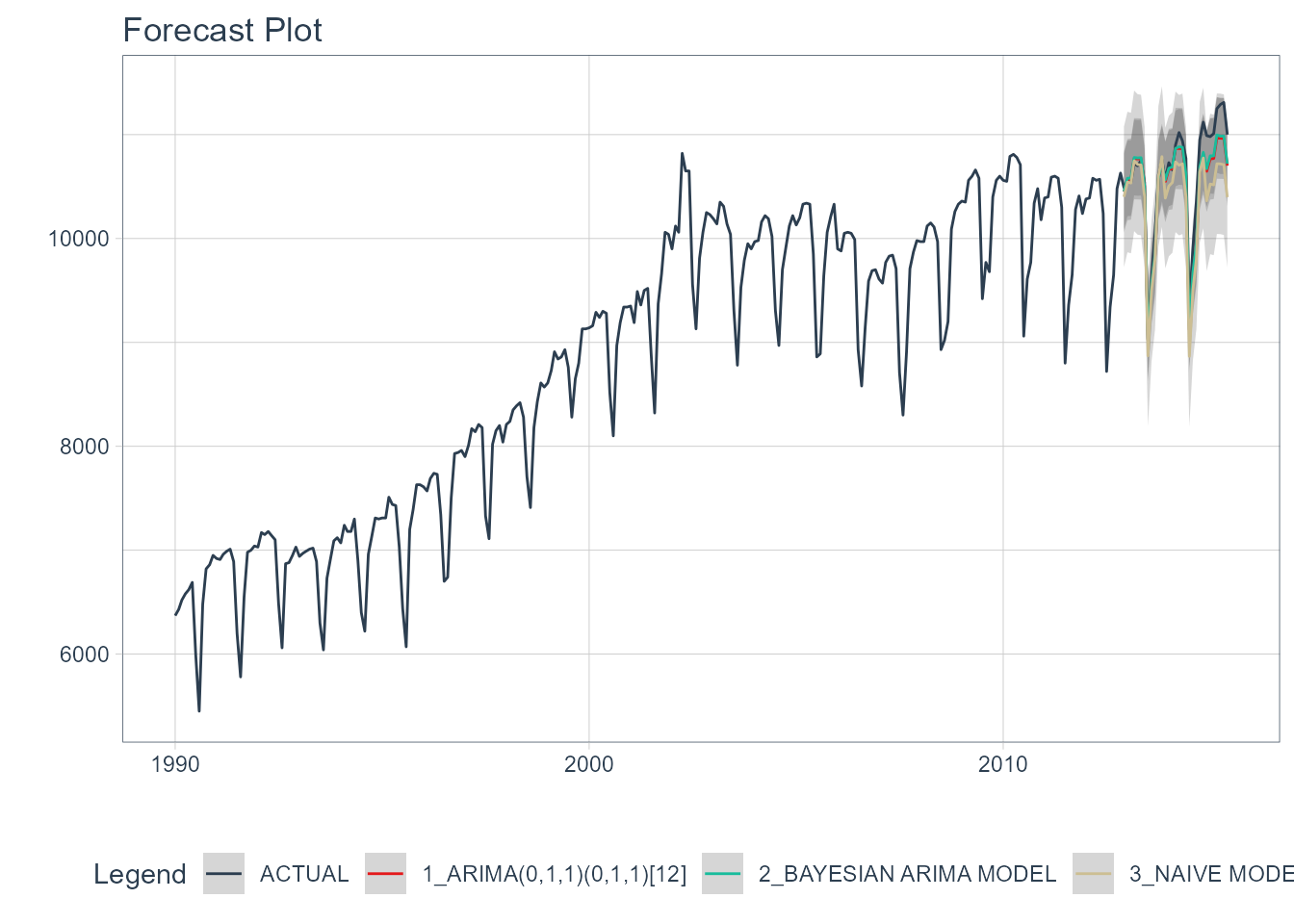
calibration_tbl %>%
    modeltime_forecast(
        new_data    = testing(splits),
        actual_data = m750
    ) %>%
    plot_modeltime_forecast(
      .legend_max_width = 25, # For mobile screens
      .interactive      = interactive
    )

5B - Accuracy Metrics

We can use modeltime_accuracy() to collect common accuracy metrics. The default reports the following metrics using yardstick functions:

• MAE - Mean absolute error, mae()
• MAPE - Mean absolute percentage error, mape()
• MASE - Mean absolute scaled error, mase()
• SMAPE - Symmetric mean absolute percentage error, smape()
• RMSE - Root mean squared error, rmse()
• RSQ - R-squared, rsq()

These of course can be customized following the rules for creating new yardstick metrics, but the defaults are very useful. Refer to default_forecast_accuracy_metrics() to learn more.

To make table-creation a bit easier, I’ve included table_modeltime_accuracy() for outputing results in either interactive (reactable) or static (gt) tables.

calibration_tbl %>%
    modeltime_accuracy() %>%
    table_modeltime_accuracy(
        .interactive = interactive
    )

Accuracy Table
.model_id	.model_desc	.type	mae	mape	mase	smape	rmse	rsq
1	ARIMA(0,1,1)(0,1,1)[12]	Test	151.33	1.41	0.52	1.43	197.71	0.93
2	BAYESIAN ARIMA MODEL	Test	142.20	1.33	0.49	1.34	184.44	0.94
3	NAIVE MODEL	Test	273.14	2.55	0.93	2.60	342.23	0.84

Step 6 - Refit to Full Dataset & Forecast Forward

The final step is to refit the models to the full dataset using modeltime_refit() and forecast them forward.

refit_tbl <- calibration_tbl %>%
    modeltime_refit(data = m750)
#> 
#> SAMPLING FOR MODEL 'Sarima' NOW (CHAIN 1).
#> Chain 1: 
#> Chain 1: Gradient evaluation took 0 seconds
#> Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0 seconds.
#> Chain 1: Adjust your expectations accordingly!
#> Chain 1: 
#> Chain 1: 
#> Chain 1: Iteration:    1 / 2000 [  0%]  (Warmup)
#> Chain 1: Iteration:  200 / 2000 [ 10%]  (Warmup)
#> Chain 1: Iteration:  400 / 2000 [ 20%]  (Warmup)
#> Chain 1: Iteration:  600 / 2000 [ 30%]  (Warmup)
#> Chain 1: Iteration:  800 / 2000 [ 40%]  (Warmup)
#> Chain 1: Iteration: 1000 / 2000 [ 50%]  (Warmup)
#> Chain 1: Iteration: 1001 / 2000 [ 50%]  (Sampling)
#> Chain 1: Iteration: 1200 / 2000 [ 60%]  (Sampling)
#> Chain 1: Iteration: 1400 / 2000 [ 70%]  (Sampling)
#> Chain 1: Iteration: 1600 / 2000 [ 80%]  (Sampling)
#> Chain 1: Iteration: 1800 / 2000 [ 90%]  (Sampling)
#> Chain 1: Iteration: 2000 / 2000 [100%]  (Sampling)
#> Chain 1: 
#> Chain 1:  Elapsed Time: 5.755 seconds (Warm-up)
#> Chain 1:                5.785 seconds (Sampling)
#> Chain 1:                11.54 seconds (Total)
#> Chain 1: 
#> 
#> SAMPLING FOR MODEL 'Sarima' NOW (CHAIN 2).
#> Chain 2: 
#> Chain 2: Gradient evaluation took 0 seconds
#> Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0 seconds.
#> Chain 2: Adjust your expectations accordingly!
#> Chain 2: 
#> Chain 2: 
#> Chain 2: Iteration:    1 / 2000 [  0%]  (Warmup)
#> Chain 2: Iteration:  200 / 2000 [ 10%]  (Warmup)
#> Chain 2: Iteration:  400 / 2000 [ 20%]  (Warmup)
#> Chain 2: Iteration:  600 / 2000 [ 30%]  (Warmup)
#> Chain 2: Iteration:  800 / 2000 [ 40%]  (Warmup)
#> Chain 2: Iteration: 1000 / 2000 [ 50%]  (Warmup)
#> Chain 2: Iteration: 1001 / 2000 [ 50%]  (Sampling)
#> Chain 2: Iteration: 1200 / 2000 [ 60%]  (Sampling)
#> Chain 2: Iteration: 1400 / 2000 [ 70%]  (Sampling)
#> Chain 2: Iteration: 1600 / 2000 [ 80%]  (Sampling)
#> Chain 2: Iteration: 1800 / 2000 [ 90%]  (Sampling)
#> Chain 2: Iteration: 2000 / 2000 [100%]  (Sampling)
#> Chain 2: 
#> Chain 2:  Elapsed Time: 1.053 seconds (Warm-up)
#> Chain 2:                0.861 seconds (Sampling)
#> Chain 2:                1.914 seconds (Total)
#> Chain 2: 
#> 
#> SAMPLING FOR MODEL 'Sarima' NOW (CHAIN 3).
#> Chain 3: 
#> Chain 3: Gradient evaluation took 0 seconds
#> Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0 seconds.
#> Chain 3: Adjust your expectations accordingly!
#> Chain 3: 
#> Chain 3: 
#> Chain 3: Iteration:    1 / 2000 [  0%]  (Warmup)
#> Chain 3: Iteration:  200 / 2000 [ 10%]  (Warmup)
#> Chain 3: Iteration:  400 / 2000 [ 20%]  (Warmup)
#> Chain 3: Iteration:  600 / 2000 [ 30%]  (Warmup)
#> Chain 3: Iteration:  800 / 2000 [ 40%]  (Warmup)
#> Chain 3: Iteration: 1000 / 2000 [ 50%]  (Warmup)
#> Chain 3: Iteration: 1001 / 2000 [ 50%]  (Sampling)
#> Chain 3: Iteration: 1200 / 2000 [ 60%]  (Sampling)
#> Chain 3: Iteration: 1400 / 2000 [ 70%]  (Sampling)
#> Chain 3: Iteration: 1600 / 2000 [ 80%]  (Sampling)
#> Chain 3: Iteration: 1800 / 2000 [ 90%]  (Sampling)
#> Chain 3: Iteration: 2000 / 2000 [100%]  (Sampling)
#> Chain 3: 
#> Chain 3:  Elapsed Time: 7.179 seconds (Warm-up)
#> Chain 3:                5.719 seconds (Sampling)
#> Chain 3:                12.898 seconds (Total)
#> Chain 3: 
#> 
#> SAMPLING FOR MODEL 'Sarima' NOW (CHAIN 4).
#> Chain 4: 
#> Chain 4: Gradient evaluation took 0 seconds
#> Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0 seconds.
#> Chain 4: Adjust your expectations accordingly!
#> Chain 4: 
#> Chain 4: 
#> Chain 4: Iteration:    1 / 2000 [  0%]  (Warmup)
#> Chain 4: Iteration:  200 / 2000 [ 10%]  (Warmup)
#> Chain 4: Iteration:  400 / 2000 [ 20%]  (Warmup)
#> Chain 4: Iteration:  600 / 2000 [ 30%]  (Warmup)
#> Chain 4: Iteration:  800 / 2000 [ 40%]  (Warmup)
#> Chain 4: Iteration: 1000 / 2000 [ 50%]  (Warmup)
#> Chain 4: Iteration: 1001 / 2000 [ 50%]  (Sampling)
#> Chain 4: Iteration: 1200 / 2000 [ 60%]  (Sampling)
#> Chain 4: Iteration: 1400 / 2000 [ 70%]  (Sampling)
#> Chain 4: Iteration: 1600 / 2000 [ 80%]  (Sampling)
#> Chain 4: Iteration: 1800 / 2000 [ 90%]  (Sampling)
#> Chain 4: Iteration: 2000 / 2000 [100%]  (Sampling)
#> Chain 4: 
#> Chain 4:  Elapsed Time: 1.188 seconds (Warm-up)
#> Chain 4:                0.92 seconds (Sampling)
#> Chain 4:                2.108 seconds (Total)
#> Chain 4: 
#> 
#> SAMPLING FOR MODEL 'Sarima' NOW (CHAIN 1).
#> Chain 1: 
#> Chain 1: Gradient evaluation took 0 seconds
#> Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0 seconds.
#> Chain 1: Adjust your expectations accordingly!
#> Chain 1: 
#> Chain 1: 
#> Chain 1: Iteration:    1 / 2000 [  0%]  (Warmup)
#> Chain 1: Iteration:  200 / 2000 [ 10%]  (Warmup)
#> Chain 1: Iteration:  400 / 2000 [ 20%]  (Warmup)
#> Chain 1: Iteration:  600 / 2000 [ 30%]  (Warmup)
#> Chain 1: Iteration:  800 / 2000 [ 40%]  (Warmup)
#> Chain 1: Iteration: 1000 / 2000 [ 50%]  (Warmup)
#> Chain 1: Iteration: 1001 / 2000 [ 50%]  (Sampling)
#> Chain 1: Iteration: 1200 / 2000 [ 60%]  (Sampling)
#> Chain 1: Iteration: 1400 / 2000 [ 70%]  (Sampling)
#> Chain 1: Iteration: 1600 / 2000 [ 80%]  (Sampling)
#> Chain 1: Iteration: 1800 / 2000 [ 90%]  (Sampling)
#> Chain 1: Iteration: 2000 / 2000 [100%]  (Sampling)
#> Chain 1: 
#> Chain 1:  Elapsed Time: 1.098 seconds (Warm-up)
#> Chain 1:                0.286 seconds (Sampling)
#> Chain 1:                1.384 seconds (Total)
#> Chain 1: 
#> 
#> SAMPLING FOR MODEL 'Sarima' NOW (CHAIN 2).
#> Chain 2: 
#> Chain 2: Gradient evaluation took 0 seconds
#> Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0 seconds.
#> Chain 2: Adjust your expectations accordingly!
#> Chain 2: 
#> Chain 2: 
#> Chain 2: Iteration:    1 / 2000 [  0%]  (Warmup)
#> Chain 2: Iteration:  200 / 2000 [ 10%]  (Warmup)
#> Chain 2: Iteration:  400 / 2000 [ 20%]  (Warmup)
#> Chain 2: Iteration:  600 / 2000 [ 30%]  (Warmup)
#> Chain 2: Iteration:  800 / 2000 [ 40%]  (Warmup)
#> Chain 2: Iteration: 1000 / 2000 [ 50%]  (Warmup)
#> Chain 2: Iteration: 1001 / 2000 [ 50%]  (Sampling)
#> Chain 2: Iteration: 1200 / 2000 [ 60%]  (Sampling)
#> Chain 2: Iteration: 1400 / 2000 [ 70%]  (Sampling)
#> Chain 2: Iteration: 1600 / 2000 [ 80%]  (Sampling)
#> Chain 2: Iteration: 1800 / 2000 [ 90%]  (Sampling)
#> Chain 2: Iteration: 2000 / 2000 [100%]  (Sampling)
#> Chain 2: 
#> Chain 2:  Elapsed Time: 0.734 seconds (Warm-up)
#> Chain 2:                0.416 seconds (Sampling)
#> Chain 2:                1.15 seconds (Total)
#> Chain 2: 
#> 
#> SAMPLING FOR MODEL 'Sarima' NOW (CHAIN 3).
#> Chain 3: 
#> Chain 3: Gradient evaluation took 0 seconds
#> Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0 seconds.
#> Chain 3: Adjust your expectations accordingly!
#> Chain 3: 
#> Chain 3: 
#> Chain 3: Iteration:    1 / 2000 [  0%]  (Warmup)
#> Chain 3: Iteration:  200 / 2000 [ 10%]  (Warmup)
#> Chain 3: Iteration:  400 / 2000 [ 20%]  (Warmup)
#> Chain 3: Iteration:  600 / 2000 [ 30%]  (Warmup)
#> Chain 3: Iteration:  800 / 2000 [ 40%]  (Warmup)
#> Chain 3: Iteration: 1000 / 2000 [ 50%]  (Warmup)
#> Chain 3: Iteration: 1001 / 2000 [ 50%]  (Sampling)
#> Chain 3: Iteration: 1200 / 2000 [ 60%]  (Sampling)
#> Chain 3: Iteration: 1400 / 2000 [ 70%]  (Sampling)
#> Chain 3: Iteration: 1600 / 2000 [ 80%]  (Sampling)
#> Chain 3: Iteration: 1800 / 2000 [ 90%]  (Sampling)
#> Chain 3: Iteration: 2000 / 2000 [100%]  (Sampling)
#> Chain 3: 
#> Chain 3:  Elapsed Time: 1.427 seconds (Warm-up)
#> Chain 3:                0.296 seconds (Sampling)
#> Chain 3:                1.723 seconds (Total)
#> Chain 3: 
#> 
#> SAMPLING FOR MODEL 'Sarima' NOW (CHAIN 4).
#> Chain 4: 
#> Chain 4: Gradient evaluation took 0 seconds
#> Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0 seconds.
#> Chain 4: Adjust your expectations accordingly!
#> Chain 4: 
#> Chain 4: 
#> Chain 4: Iteration:    1 / 2000 [  0%]  (Warmup)
#> Chain 4: Iteration:  200 / 2000 [ 10%]  (Warmup)
#> Chain 4: Iteration:  400 / 2000 [ 20%]  (Warmup)
#> Chain 4: Iteration:  600 / 2000 [ 30%]  (Warmup)
#> Chain 4: Iteration:  800 / 2000 [ 40%]  (Warmup)
#> Chain 4: Iteration: 1000 / 2000 [ 50%]  (Warmup)
#> Chain 4: Iteration: 1001 / 2000 [ 50%]  (Sampling)
#> Chain 4: Iteration: 1200 / 2000 [ 60%]  (Sampling)
#> Chain 4: Iteration: 1400 / 2000 [ 70%]  (Sampling)
#> Chain 4: Iteration: 1600 / 2000 [ 80%]  (Sampling)
#> Chain 4: Iteration: 1800 / 2000 [ 90%]  (Sampling)
#> Chain 4: Iteration: 2000 / 2000 [100%]  (Sampling)
#> Chain 4: 
#> Chain 4:  Elapsed Time: 1.056 seconds (Warm-up)
#> Chain 4:                0.284 seconds (Sampling)
#> Chain 4:                1.34 seconds (Total)
#> Chain 4:
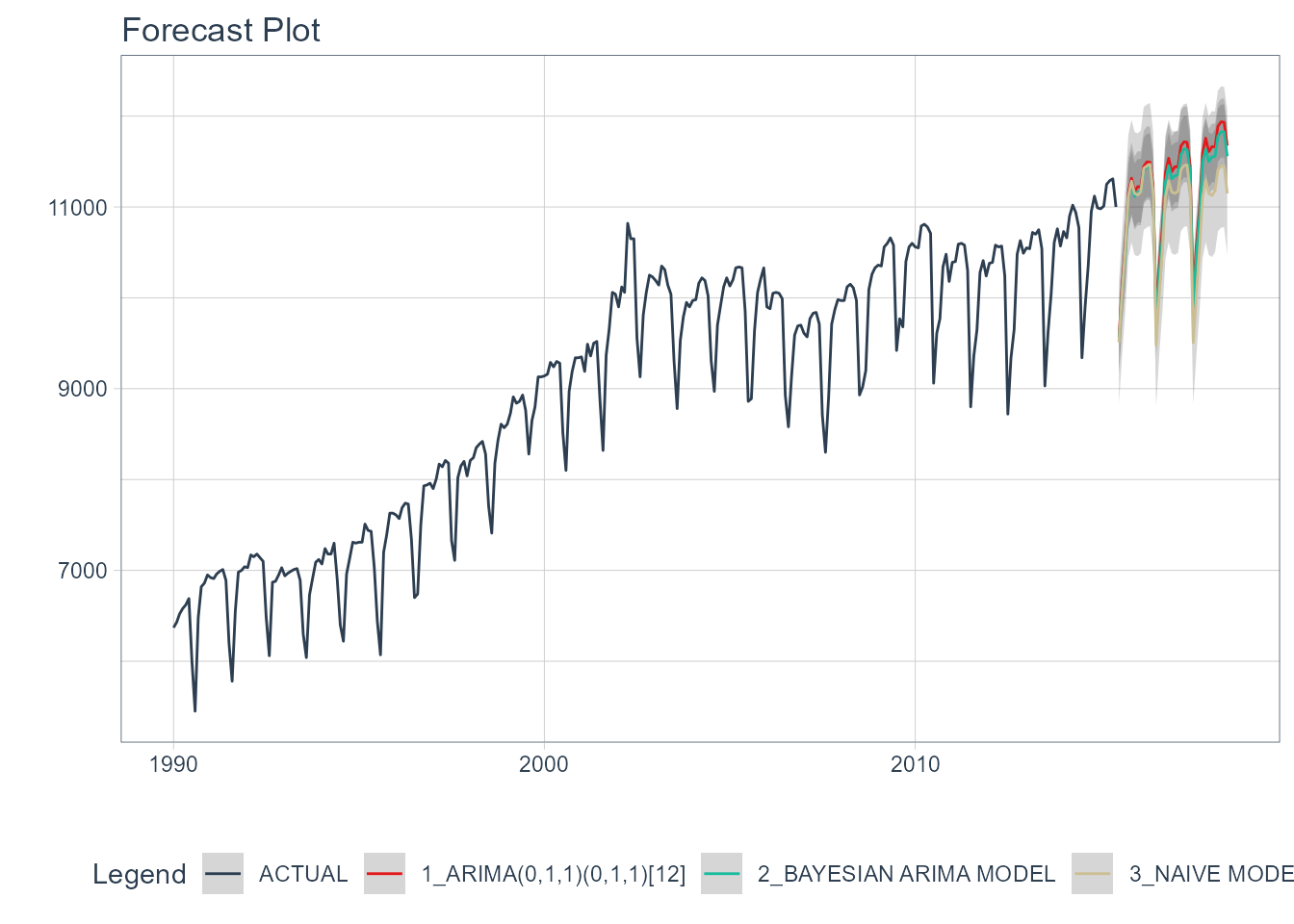
refit_tbl %>%
    modeltime_forecast(h = "3 years", actual_data = m750) %>%
    plot_modeltime_forecast(
      .legend_max_width = 25, # For mobile screens
      .interactive      = interactive
    )